فرمول های فیزیک :: علوم هشتم

فرمول های فیزیک

دوشنبه, ۲۷ مرداد ۱۳۹۳، ۰۶:۰۲ ب.ظ

ین مقاله می‌کوشد فهرستی از فرمول‌هایِ اولیه‌یِ فیزیک را ارائه کند، فرمول‌هایی که در دوره‌هایِ مقدماتیِ دبیرستانی و دانشگاهی، تدریس می‌شوند. در این مقاله، اصل‌ها به رنگ سبز، تعریف‌ها به رنگ آبی و قضیه‌ها به رنگِ سیاه، مشخص شده‌اند.

پیشوندهایِ سامانه‌یِ متریک

پیشوندهای اس‌آی
پیشوند	نماد	۱۰۰۰^m	۱۰ⁿ	اعشاری	مقیاس کوچک	مقیاس بزرگ	از
یوتا	Y	۱۰۰۰^۸	۱۰^۲۴	۱۰۰۰۰۰۰۰۰۰۰۰۰۰۰۰۰۰۰۰۰۰۰۰۰	سپتیلیون	کوادرلیون	۱۹۹۱
زتا	Z	۱۰۰۰^۷	۱۰^۲۱	۱۰۰۰۰۰۰۰۰۰۰۰۰۰۰۰۰۰۰۰۰۰	سکستیلیون	تریلیارد	۱۹۹۱
اگزا	E	۱۰۰۰^۶	۱۰^۱۸	۱۰۰۰۰۰۰۰۰۰۰۰۰۰۰۰۰۰۰	کوئینتیلیون	تریلیون	۱۹۷۵
پتا	P	۱۰۰۰^۵	۱۰^۱۵	۱۰۰۰۰۰۰۰۰۰۰۰۰۰۰۰	کوادریلیون	بیلیارد	۱۹۷۵
ترا	T	۱۰۰۰^۴	۱۰^۱۲	۱۰۰۰۰۰۰۰۰۰۰۰۰	تریلیون	میلیارد	۱۹۶۰
گیگا	G	۱۰۰۰^۳	۱۰^۹	۱۰۰۰۰۰۰۰۰۰	میلیارد		۱۹۶۰
مگا	M	۱۰۰۰^۲	۱۰^۶	۱۰۰۰۰۰۰	میلیون		۱۹۶۰
کیلو	k	۱۰۰۰^۱	۱۰^۳	۱۰۰۰	هزار		۱۷۹۵
هکتو	h	۱۰۰۰^۲/۳	۱۰^۲	۱۰۰	صد		۱۷۹۵
دکا	da	۱۰۰۰^۱/۳	۱۰^۱	۱۰	ده		۱۷۹۵
یونی	u	۱۰۰۰^۰	۱۰^۰	۱	یک		–
دسی	d	۱۰۰۰^−۱/۳	۱۰^−۱	۰٫۱	دهم		۱۷۹۵
سانتی	c	۱۰۰۰^−۲/۳	۱۰^−۲	۰٫۰۱	صدم		۱۷۹۵
میلی	m	۱۰۰۰^−۱	۱۰^−۳	۰٫۰۰۱	هزارم		۱۷۹۵
میکرو	μ	۱۰۰۰^−۲	۱۰^−۶	۰٫۰۰۰۰۰۱	میلیونیوم		۱۹۶۰
نانو	n	۱۰۰۰^−۳	۱۰^−۹	۰٫۰۰۰۰۰۰۰۰۱	میلیاردیوم		۱۹۶۰
پیکو	p	۱۰۰۰^−۴	۱۰^−۱۲	۰٫۰۰۰۰۰۰۰۰۰۰۰۱	تریلیونیوم	بیلیونیوم	۱۹۶۰
فمتو	f	۱۰۰۰^−۵	۱۰^−۱۵	۰٫۰۰۰۰۰۰۰۰۰۰۰۰۰۰۱	کوادرلیونیوم	بیلیاردیوم	۱۹۶۴
آتو	a	۱۰۰۰^−۶	۱۰^−۱۸	۰٫۰۰۰۰۰۰۰۰۰۰۰۰۰۰۰۰۰۱	کوئینتلنیوم	تریلیونیوم	۱۹۶۴
زپتو	z	۱۰۰۰^−۷	۱۰^−۲۱	۰٫۰۰۰۰۰۰۰۰۰۰۰۰۰۰۰۰۰۰۰۰۱	سکسیتلنیوم	تریلیاردیوم	۱۹۹۱
یوکتو	y	۱۰۰۰^−۸	۱۰^−۲۴	۰٫۰۰۰۰۰۰۰۰۰۰۰۰۰۰۰۰۰۰۰۰۰۰۰۱	سپتیلیونیوم	کوادرلیونیوم	۱۹۹۱

قوانینِ پایه‌ایِ مکانیک[ویرایش]

معادله‌های مکانیکیِ پایه برایِ هر دو حالتِ حرکتِ انتقالی و حرکتِ دورانی.

کمیت	انتقال	دوران
زمان	$t$	$t$
مکان	$x$	$\theta$ به رادیان
جرم	$m$	$m$
مدت زمان	$\Delta t$	$\Delta t$
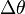جابه‌جایی	$\Delta x$	$\Delta \theta$
پایستگی جرم	$\Delta m = 0$	$\Delta m = 0$
پایستگی انرژی	$\Delta E = 0$	$\Delta E = 0$
پایستگی تکانه	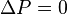$\Delta P = 0$	$\Delta L = 0$
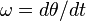سرعت	$v = dx/dt$	$\omega = d\theta/dt$
شتاب	$a = dv/dt$	$\alpha = d\omega/dt$
تکان	$j = da/dt$	$j = d\alpha/dt$
تغییرِ انرژی پتانسیل	$\Delta U = -W$	$\Delta U = -W$
تکانه	$P = mv$	${\color{Blue}L = I\omega} =\|\| \mathbf{r} \times \mathbf{P}\|\| = m\|\| \mathbf{r} \times \mathbf{v}\|\|$
نیرو	${\color{blue}f = dP/dt } = ma = -dU/dx$	${\color{blue}\tau = dL/dt } = I\alpha =\|\| \mathbf{r} \times \mathbf{f}\|\|=m\|\| \mathbf{r} \times \mathbf{a}\|\|$
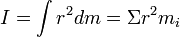لختی	$m = \int dm = \Sigma m_i$	$I = \int r^2 dm = \Sigma r^2m_i$
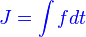ضربه	${\color{blue}J=\int f dt}$	${\color{blue}J=\int \tau dt}$
کار	${\color{blue}W = \int f dx } = \mathbf{d} \cdot \mathbf{f}$	${\color{blue}W = \int \tau d\theta }$
توان	${\color{blue} P = dW/dt } = fv$	${\color{blue} P = dW/dt } = \tau\omega$
انرژی جنبشی	$K = mv^2/2 = P^2/2m$	$K = I\omega^2/2$
قانون سوم نیوتون	$f_{ab} = - f_{ba}$	$\tau_{ab} = -\tau_{ba}$

به هر نیرویِ پایستار، یک انرژیِ پتانسیل منسوب می‌کنیم. برایِ آن‌که خودِ انرژیِ پتانسیل (و نه تغییرِ آن) را به شکلی مستقل به دست آوریم از قاعده‌یِ زیر استفاده می‌کنیم:

هر کجا که نیرو صفر است، انرژیِ پتانسیل را هم صفر در نظر می‌گیریم. این نقطه را مبدا گرفته و انرژیِ پتانسیلِ سایرِ نقطه‌ها را نسبت به آن به دست می‌آوریم.

شتاب ثابت

معادله‌هایِ حرکت در هر دو حالتِ انتقال و دوران، برای حالتی که شتاب ثابت است:

کمیت	انتقال	دوران
جابه‌جایی	$\Delta v = at$	$\Delta \omega = \alpha t$
مستقل از زمان	$\Delta v^2-v_{0}^2 = 2a\Delta x$	$\Delta\omega^2 = 2\alpha\Delta \theta$
شتاب	$\Delta x = t\Delta v/2$	$\Delta \theta = t\Delta \omega/2$
سرعت نهایی	$\Delta x = -at^2/2 + v_2t$	$\Delta \theta = -\alpha t^2/2 + \omega_2t$
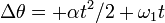سرعتِ اولیه	$\Delta x = +at^2/2 + v_1t$	$\Delta \theta = +\alpha t^2/2 + \omega_1t$